250x250
Notice
Recent Posts
Recent Comments
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 프로그래머스 알고리즘
- 막무가내
- 막내의막무가내 안드로이드
- 부스트코스
- 막내의막무가내 플러터
- 막내의막무가내 회고 및 목표
- 부스트코스에이스
- 안드로이드
- Fragment
- 주엽역 생활맥주
- 막내의막무가내 코틀린 안드로이드
- 안드로이드 sunflower
- 막내의막무가내 안드로이드 에러 해결
- 막내의막무가내 목표 및 회고
- 막내의막무가내 플러터 flutter
- 막내의막무가내 알고리즘
- flutter network call
- 막내의막무가내 rxjava
- 막내의막무가내 SQL
- 2022년 6월 일상
- 안드로이드 Sunflower 스터디
- 막내의 막무가내 알고리즘
- 프래그먼트
- 막내의막무가내 일상
- 막내의막무가내
- 막내의 막무가내
- 막내의막무가내 코볼 COBOL
- 막내의막무가내 프로그래밍
- 막내의막무가내 코틀린
- 막내의막무가내 안드로이드 코틀린
Archives
- Today
- Total
막내의 막무가내 프로그래밍 & 일상
[알고리즘] 백준 1956 운동 -플로이드 워셜- 자바 코틀린 본문
728x90
1956번: 운동
첫째 줄에 V와 E가 빈칸을 사이에 두고 주어진다. (2 ≤ V ≤ 400, 0 ≤ E ≤ V(V-1)) 다음 E개의 줄에는 각각 세 개의 정수 a, b, c가 주어진다. a번 마을에서 b번 마을로 가는 거리가 c인 도로가 있다는 의
www.acmicpc.net
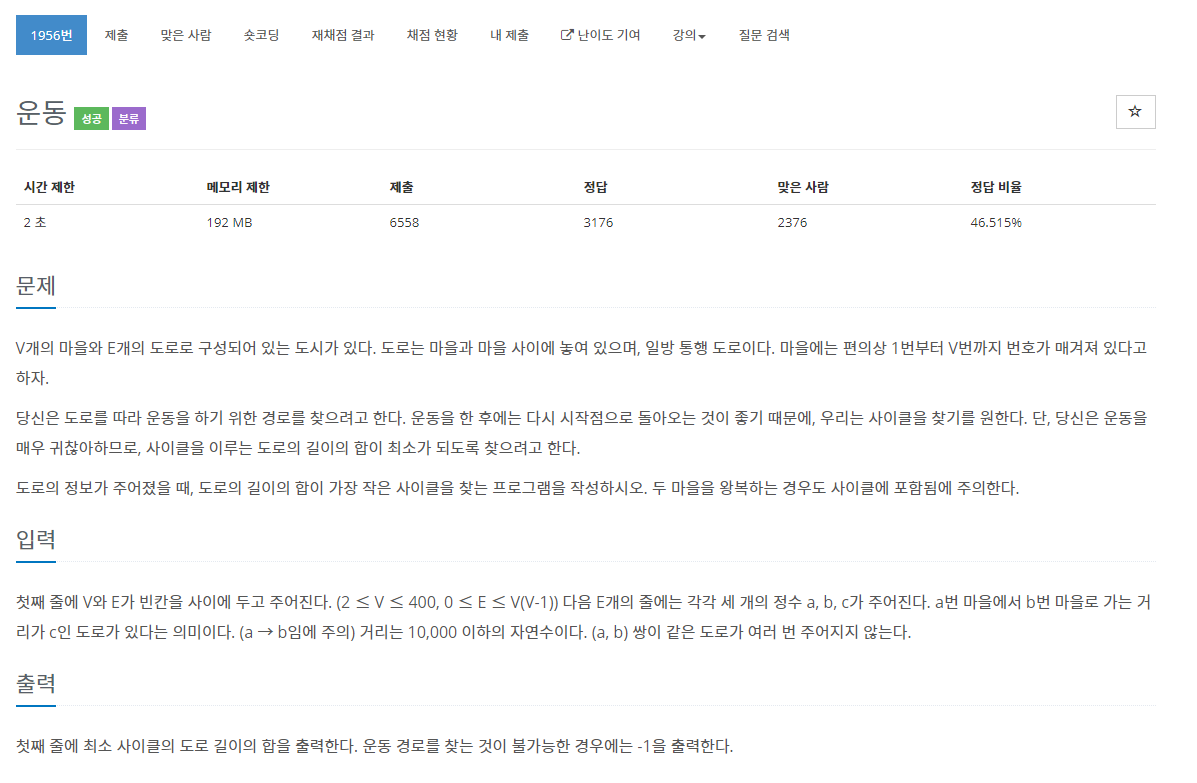

백준 플로이드 워셜 알고리즘 유형인 운동 문제를 풀어봤습니다. ㅎㅎ
마을과 연결된(단방향) 도로가 있는데 모든 마을을 최소거리(비용)로 도는 비용을 출력해야합니다. (사이클이 존재하지않는다면 -1 출력)
플로이드 유형을 골라푼만큼 플로이드를 사용해서 모든 정점 사이의 최단경로를 구해서 풀이했습니다.
또한 이전문제들과 다르게 자기 자신에 대한 경로를 0이 아닌 INF로 세팅하여 자기 자신의 값도 갱신되게 플로이드 알고리즘 수행 후 자신~자기 자신의 도로 길이의 최솟값을 찾으면 된다.
(i, i) -> i에서 i가 INF가 아니면 i->i 즉 자기 자신에서 출발해서 자기 자신에게 돌아왔다는 뜻으로 사이클이 존재한다.
풀이는 다음과 같습니다.
[Java]
import java.util.Arrays;
import java.util.Scanner;
class Main {
private static int V; // V개의 마을
private static int E; // E개의 도로
private static int[][] distance; // 도로의 최소거리
private static int INF = 10000 * 400 + 1;
private static int answer = 10000 * 400 + 1;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
V = sc.nextInt();
E = sc.nextInt();
distance = new int[V + 1][V + 1];
//초기화
for (int i = 1; i <= V; i++) {
Arrays.fill(distance[i], INF);
}
for (int i = 0; i < E; i++) {
int start = sc.nextInt(); // a번 마을
int end = sc.nextInt(); // b번 마을
int cost = sc.nextInt();
distance[start][end] = cost; //(a, b) 쌍이 같은 도로가 여러 번 주어지지 않는다.
// distance[end][start] = cost; // (a → b임에 주의)
}
floyd();
// 최소 사이클 중 최솟값을 구한다.
for (int i = 1; i <= V; i++) {
answer = Math.min(distance[i][i], answer);
}
if (answer == INF) {
System.out.println(-1);
} else {
System.out.println(answer);
}
}
private static void floyd() {
for (int k = 1; k <= V; k++) {
for (int i = 1; i <= V; i++) {
for (int j = 1; j <= V; j++) {
distance[i][j] = Math.min(distance[i][k] + distance[k][j], distance[i][j]);
}
}
}
}
}
[Kotlin]
import java.util.*
private var V // V개의 마을
= 0
private var E // E개의 도로
= 0
private lateinit var distance // 도로의 최소거리
: Array<IntArray>
private const val INF = 10000 * 400 + 1
private var answer = 10000 * 400 + 1
fun main(args: Array<String>) {
val sc = Scanner(System.`in`)
V = sc.nextInt()
E = sc.nextInt()
distance = Array(V + 1) { IntArray(V + 1) }
//초기화
for (i in 1..V) {
Arrays.fill(distance[i], INF)
}
for (i in 0 until E) {
val start = sc.nextInt() // a번 마을
val end = sc.nextInt() // b번 마을
val cost = sc.nextInt()
distance[start][end] = cost //(a, b) 쌍이 같은 도로가 여러 번 주어지지 않는다.
// distance[end][start] = cost; // (a → b임에 주의)
}
floyd()
// 최소 사이클 중 최솟값을 구한다.
for (i in 1..V) {
answer = distance[i][i].coerceAtMost(answer)
}
if (answer == INF) {
println(-1)
} else {
println(answer)
}
}
fun floyd() {
for (k in 1..V) {
for (i in 1..V) {
for (j in 1..V) {
distance[i][j] = Math.min(distance[i][k] + distance[k][j], distance[i][j])
}
}
}
}
댓글과 공감은 큰 힘이 됩니다. 감사합니다. !!!
728x90
'알고리즘 > 플로이드 워셜' 카테고리의 다른 글
| [알고리즘] 프로그래머스 순위 -그래프, 플로이드 워셜- 자바 코틀린 (0) | 2021.05.09 |
|---|---|
| [알고리즘] 백준 10159 저울 -플로이드 워셜- 자바 코틀린 (2) | 2021.04.10 |
| [알고리즘] 백준 1389 케빈 베이컨의 6단계 법칙 -플로이드 워셜- 자바 (0) | 2021.03.31 |
| [알고리즘] 백준 11404 플로이드 -플로이드 워셜- 자바 (4) | 2021.03.30 |
Comments




