250x250
Notice
Recent Posts
Recent Comments
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 프래그먼트
- 막내의막무가내 코볼 COBOL
- 막내의막무가내 안드로이드 코틀린
- 막내의막무가내 코틀린
- 부스트코스에이스
- 막내의막무가내 플러터 flutter
- 막내의막무가내 rxjava
- Fragment
- 안드로이드 Sunflower 스터디
- 막내의막무가내 회고 및 목표
- 프로그래머스 알고리즘
- 2022년 6월 일상
- 안드로이드 sunflower
- 막내의 막무가내
- 부스트코스
- 막내의막무가내 프로그래밍
- 막내의막무가내 플러터
- 막내의 막무가내 알고리즘
- 막내의막무가내
- 막내의막무가내 안드로이드
- 주엽역 생활맥주
- 막내의막무가내 알고리즘
- 막무가내
- 막내의막무가내 SQL
- 막내의막무가내 안드로이드 에러 해결
- 막내의막무가내 일상
- 안드로이드
- 막내의막무가내 코틀린 안드로이드
- flutter network call
- 막내의막무가내 목표 및 회고
Archives
- Today
- Total
막내의 막무가내 프로그래밍 & 일상
[알고리즘] 백준 1504 특정한 최단 경로 -최단경로, 다익스트라- 자바 본문
728x90
1504번: 특정한 최단 경로
첫째 줄에 정점의 개수 N과 간선의 개수 E가 주어진다. (2 ≤ N ≤ 800, 0 ≤ E ≤ 200,000) 둘째 줄부터 E개의 줄에 걸쳐서 세 개의 정수 a, b, c가 주어지는데, a번 정점에서 b번 정점까지 양방향 길이 존
www.acmicpc.net
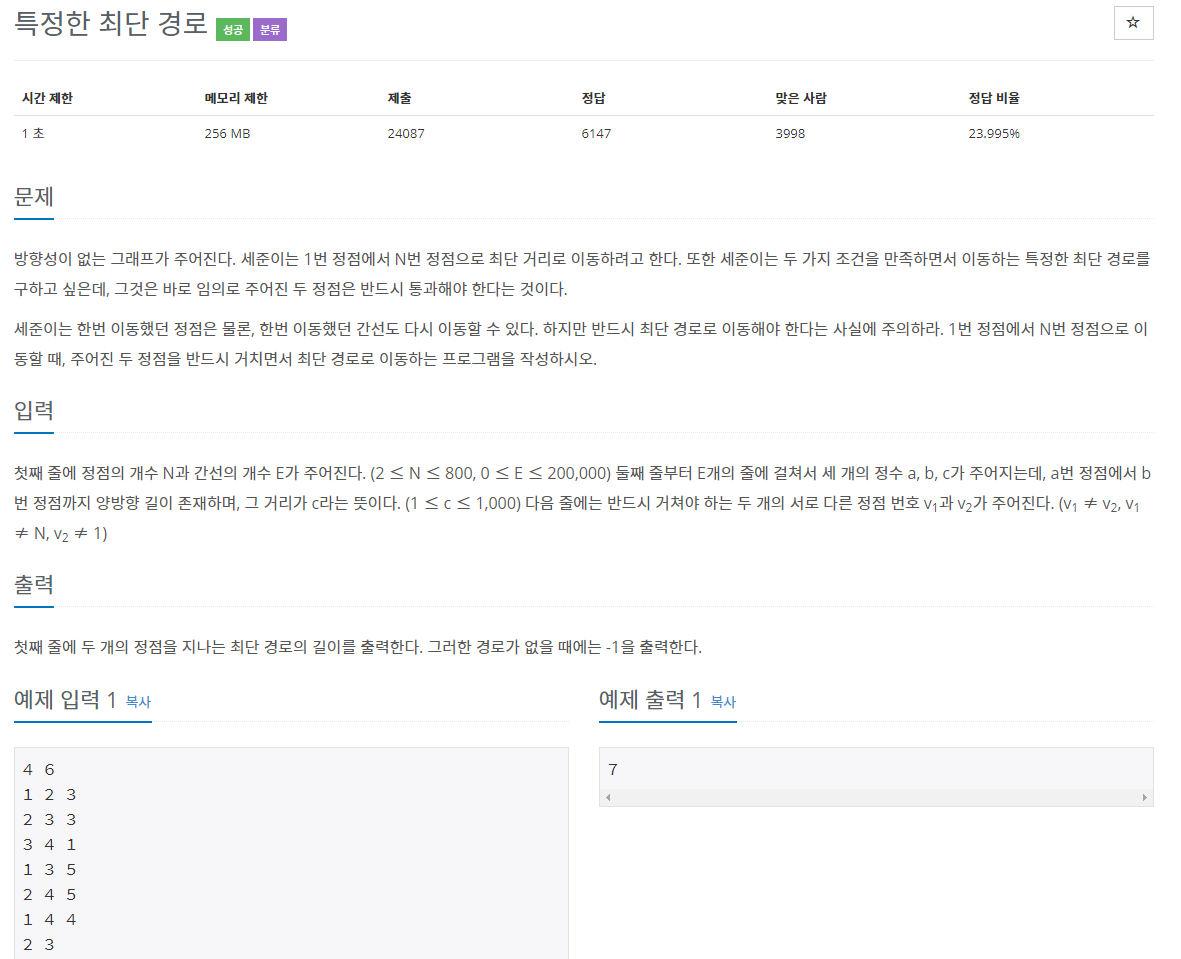
백준 최단경로 단계별풀기 두 번째 문제를 풀어봤습니다.
시작점에서 도착점까지의 최단 경로를 구해야하는데 반드시 거쳐야 할 정점 두 개를 조건으로 추가되었습니다.
반드시 지나야하는 정점이 v1, v2 인데
start -> v1 -> v2 -> end
start -> v2 -> v1 -> end
두 가지 로직이 가능합니다.
이를 적용한 풀이입니다.
[Java]
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;
class Main {
static ArrayList<Node>[] list;
private static int n;
private static int e;
private static int[] distance;
private static int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt(); //정점개수
e = sc.nextInt(); //간선개수
list = new ArrayList[n + 1]; //정점 인접리스트
distance = new int[n + 1]; //시작점과 다른 정점간의 최단경로
for (int i = 1; i <= n; i++) {
list[i] = new ArrayList<>();
}
//초기화
for (int i = 0; i < e; i++) {
int a = sc.nextInt(); //출발
int b = sc.nextInt(); //도착지
int c = sc.nextInt(); //가중치
list[a].add(new Node(b, c));
list[b].add(new Node(a, c));
}
int v1 = sc.nextInt(); //꼭 지나야하는 정점(v1 ≠ v2, v1 ≠ N, v2 ≠ 1)
int v2 = sc.nextInt();
long answer1 = 0; // 1->v1->v2->n
answer1 += dijkstra(1, v1);
answer1 += dijkstra(v1, v2);
answer1 += dijkstra(v2, n);
long answer2 = 0; // 1->v2->v1->n
answer2 += dijkstra(1, v2);
answer2 += dijkstra(v2, v1);
answer2 += dijkstra(v1, n);
if (Math.min(answer1, answer2) >= INF) {
System.out.println(-1);
return;
}
System.out.println(Math.min(answer1, answer2));
}
private static int dijkstra(int start, int end) {
distance = new int[n + 1];
Arrays.fill(distance, INF);
distance[start] = 0;
PriorityQueue<Node> queue = new PriorityQueue<>();
queue.add(new Node(start, 0));
while (!queue.isEmpty()) {
Node node = queue.poll();
int vertex = node.vertex;
int weight = node.weight;
if (distance[vertex] < weight) { //지금께 더 가중치가 크면 갱신할 필요가 없다.
continue;
}
for (int i = 0; i < list[vertex].size(); i++) {//해당 정점과 연결된 것들 탐색
int vertex2 = list[vertex].get(i).vertex;
int weight2 = list[vertex].get(i).weight + weight;
if (distance[vertex2] > weight2) { //지금께 더 최단경로라면 갱신해준다.
distance[vertex2] = weight2;
queue.add(new Node(vertex2, weight2));
}
}
}
return distance[end];
}
private static class Node implements Comparable<Node> { //우선순위큐로 성능개선(안하면 시간초과뜸)
int vertex;
int weight;
Node(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return weight - o.weight;
}
}
}
[2020-12-17]
이와 비슷하면서 더 쉬운 문제로 다음 문제가 있습니다.
위 문제와 다르게 한 정점에서 다른 정점까지의 거리만 구하면 됩니다.
1916번: 최소비용 구하기
첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그
www.acmicpc.net
이 문제의 풀이는 다음과 같습니다.
[Java]
import java.util.*;
class Main {
private static int N;
private static int M;
private static int INF = Integer.MAX_VALUE;
private static int[] distance;
private static List<Edge>[] edgeList;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
M = sc.nextInt();
distance = new int[N + 1];
edgeList = new ArrayList[N + 1];
Arrays.fill(distance, INF);
for (int i = 1; i <= N; i++) {
edgeList[i] = new ArrayList<>();
}
for (int i = 0; i < M; i++) {
int start = sc.nextInt();
int end = sc.nextInt();
int weight = sc.nextInt();
edgeList[start].add(new Edge(end, weight));
}
int start = sc.nextInt();
int end = sc.nextInt();
dijkstra(start, end);
System.out.println(distance[end]);
}
private static void dijkstra(int start, int end) {
PriorityQueue<Edge> queue = new PriorityQueue<>();
distance[start] = 0;
queue.offer(new Edge(start, 0));
while (!queue.isEmpty()) {
Edge edge = queue.poll();
int vertex = edge.vertex;
int weight = edge.weight;
if (distance[vertex] < weight) {
continue;
}
for (int i = 0; i < edgeList[vertex].size(); i++) {
int vertex2 = edgeList[vertex].get(i).vertex;
int weight2 = edgeList[vertex].get(i).weight + weight;
if (distance[vertex2] > weight2) {
distance[vertex2] = weight2;
queue.offer(new Edge(vertex2, weight2));
}
}
}
}
private static class Edge implements Comparable<Edge> {
int vertex;
int weight;
public Edge(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
@Override
public int compareTo(Edge e) {
return weight - e.weight;
}
}
}
댓글과 공감은 큰 힘이 됩니다. 감사합니다. !!
728x90
'알고리즘 > 다익스트라' 카테고리의 다른 글
| [알고리즘] 백준 4485 녹색 옷 입은 애가 젤다지? -다익스트라 + BFS, 최단경로 - 자바 코틀린 (0) | 2021.04.12 |
|---|---|
| [알고리즘] 백준 18352 특정 거리의 도시 찾기 -최단경로, 다익스트라- 자바 (0) | 2021.04.11 |
| [알고리즘] 프로그래머스 배달 -최단경로, 다익스트라- 자바Summer/Winter Coding(~2018) (0) | 2021.03.24 |
| [알고리즘] 백준 11779 최소비용 구하기 2 -다익스트라, 최단경로- (2) | 2020.12.27 |
| [알고리즘] 백준 1753 최단경로 -최단경로, 다익스트라, 그래프- 자바 (0) | 2020.11.26 |
Comments




